
向量法是解高中立体几何题的神器。只要能建立空间直角坐标系的题,都可以用向量法来解,而这样的题目可以占到所有立体几何题的 95% 以上。与传统方法相比,向量法的计算量稍微大一些,但它的优点是不需要费脑筋做辅助线,而只需要简单粗暴地按套路进行计算,所以尤其适用于复杂的问题。
向量法的完整套路中,包含一种名为「叉积」的运算,它在部分地区是超出教学大纲的。但是没有「叉积」的向量法在很多情况下发挥不出它的魔力。本文就来把「叉积」这个缺口补上,让大家领略一下向量法的简单、粗暴、有效。当然啦,我知道你们会有「考试时不让用叉积」的抱怨。没关系,我会教你怎样把叉积「伪装」成不超纲的内容。
本文的第一部分将介绍向量间的点积、叉积两种运算,包括它们的定义、计算公式、运算律,以及向量法中直线和平面的方向的表示方法。高中立体几何题的大部分问题都是求角或求距离,本文的第二、三部分就来介绍各种角和距离用向量法怎么求。证明题一般是要证明线、面之间的平行或垂直,或者两个角的大小、两条线段的长度相等,都可以化归成求角或求距离。在第四部分,我会讲一下叉积在求面积、求体积这两种相对罕见的题型中的用法。最后展示一道例题。
一、基础知识
1.1 向量的点积运算
向量的点积是大纲之内的内容。设两个向量为
点积运算适用于任何维度的向量,不过本文只讨论三维情况。在空间直角坐标系中,设
向量的点积具有交换律和分配律:
-
- 交换律:
- 分配律:
- 交换律:
但没有结合律,因为两个向量的点积是一个数,不能再与第三个向量进行点积运算。
1.2 向量的叉积运算
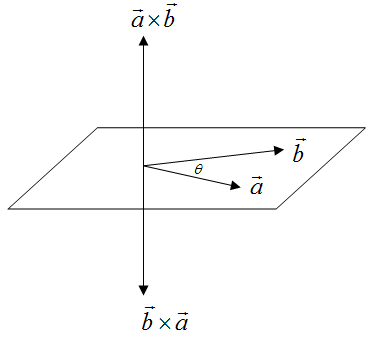
向量的叉积是本文要介绍的重点。叉积仅对三维向量有定义。设两个三维向量为
-
- 它的模等于
各自的模之积再乘以夹角的正弦,即
;
- 它的方向与
右手定则,如下图所示。
都垂直,且满足
- 它的模等于
右手定则有两种理解方式,如下图。一种是:伸出拇指和食指,让它们分别朝向
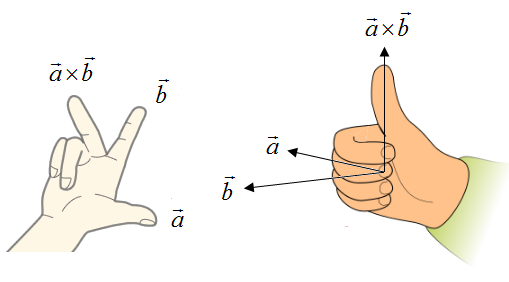
当
在空间直角坐标系中,设
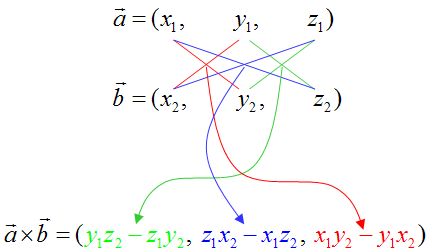
注意,左、右两个交叉相乘是「捺减撇」,中间的交叉相乘是「撇减捺」。
向量的叉积具有反交换律和分配律:
-
- 反交换律:
- 分配律:
- 反交换律:
两个向量的叉积是一个向量,可以继续与第三个向量进行叉积运算,但不幸的是,叉积运算也不满足结合律,即没有
1.3 直线与平面方向的表示
在能建立空间直角坐标系的题目中,提到一条直线,一定会已知直线上两点
而平面的方向,则是用与平面垂直的向量来表示的,这个向量称为「法向量」。提到一个平面,一定会已知平面上不共线的三点
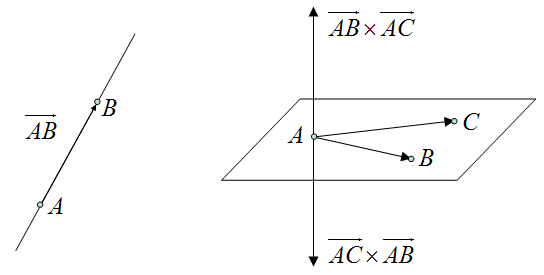
在立体几何题中,叉积的主要用途就是求平面的法向量。如果考试时不允许在步骤中使用叉积运算,可以用如下方法绕过去:既然法向量就是与平面中两个已知向量都垂直的向量,那么可以设出法向量
★![]()
在试卷上列出这个方程组后,不必真正去解它,而是在草稿纸上根据
二、用向量法求各种角
高中立体几何涉及的角度有:线线角、线面角、面面角。
2.1 求两条直线的夹角
设两条直线的方向向量分别为

有同学要问了:上面的方法利用的是点积,那么利用叉积求得两条直线的夹角为
注意向量法并不要求两条直线共面,它同样适用于异面直线!这就避免了传统方法中作平行线的麻烦。
2.2 求直线与平面的夹角
设直线的方向向量为
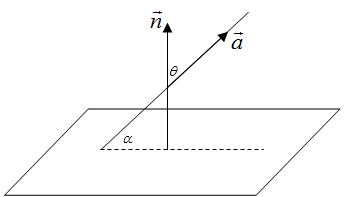
请再次领略向量法的简单粗暴有效:传统方法中,要求线面角,必须找到直线与平面的交点,并作出直线在平面内的投影。而在向量法中,只要知道直线上的任意两点和平面中任意三点(不共线)的坐标,就可以代入公式计算出直线的方向向量和平面的法向量,再代入公式计算夹角,完全不必考虑五个已知点的位置关系。
2.3 求两个平面的夹角
设两个平面的法向量分别为
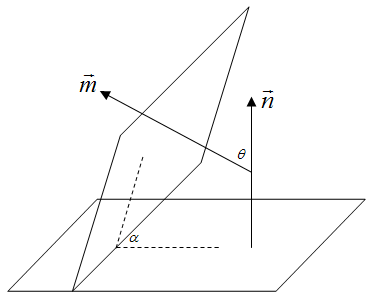
在几何题中,提到「二面角」,往往指的不是两个「平面」的夹角,而是两个「半平面」的夹角——也就是说,求的是
用向量法求二面角,同样不需要找到两个面的交线和它在两个面内的垂线,而只需要知道两个面内六个点的坐标。在很多情况下,交线上会有两个已知点,那么就只需要在两个面中各再找一个点。
三、用向量法求各种距离
点、线、面三种图形两两组合,可以得到六种距离:两点距、点线距、点面距、线线距、线面距、面面距。其中线面距、面面距只在线面或面面平行时才有定义,此时可以在直线或其中一个平面中任取一点,转化为点面距。因此这一部分将介绍前四种距离的求法。
3.1 求两点间的距离
设两点的坐标分别为
3.2 求点到直线的距离
如图,设直线上任意一点到已知点的向量为
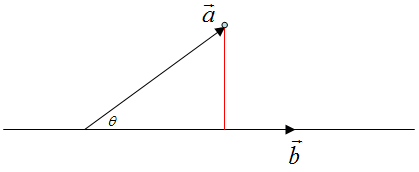
这里为什么使用了计算量大的叉积,而不是点积呢?这是为了利用叉积定义中现成的
3.3 求点到平面的距离
如图,设平面上任意一点到已知点的向量为
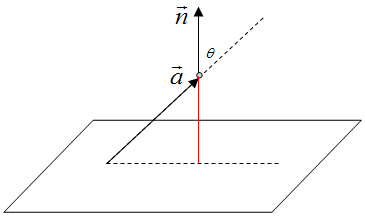
点到平面的距离,其实是向量
3.4 求两条直线的距离
三维空间中直线有三种位置关系:相交、平行、异面。后两种情况都可以求距离,但方法不一样。若两条直线平行,则可在其中一条直线上任取一点,转化成求该点到另一条直线的距离。若两条直线异面,则可以按如下步骤求出它们的距离。设第一条直线上有两个已知点
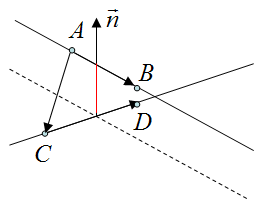
我们看到,两条直线的位置关系不同时,它们的距离求法不一样。但向量法最有用的时候,正是图形的位置关系不清楚的时候。有没有简便的方法判断直线的位置关系呢?有!先不管三七二十一地计算「法向量」
四、用向量法求三角形面积和四面体体积
这两种题型在高中立体几何中出现的频率不高,但它们与高等数学中「行列式」的概念联系紧密,有兴趣的同学可以涉猎一下。
4.1 求三角形的面积
设三角形三个顶点
这个公式同样适用于平面几何,此时
把
4.2 求四面体的体积
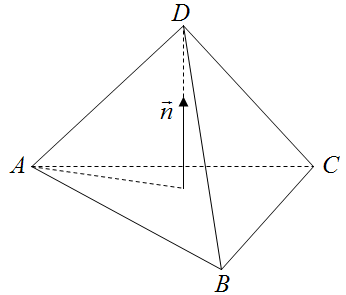
设四面体四个顶点
上述结果去掉
设
行列式的概念还可以推广到更高维的空间。从同一个点出发的
五、一道例题

图中是一座金字塔。它是一个正四棱锥,底面
-
- 求金字塔相邻侧面所成的二面角
。
- 求金字塔的棱
所在直线与底边
所在直线的距离。
- 求火苗
到棱
所在直线的距离。
- 求金字塔相邻侧面所成的二面角
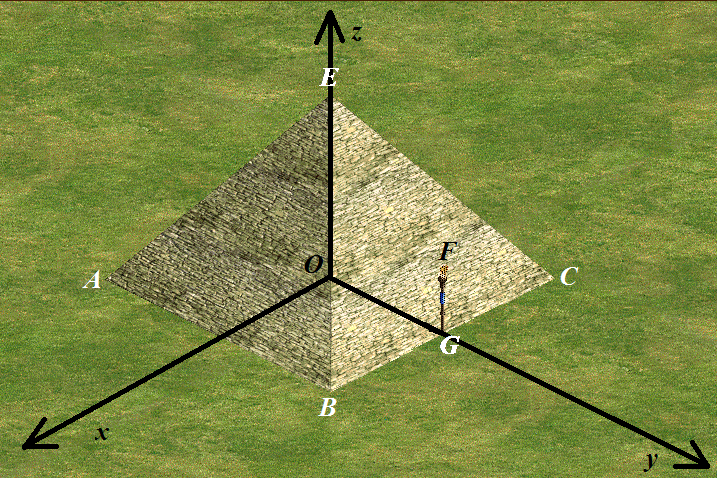
解:如上图建立空间直角坐标系,原点
求二面角
求直线
求点




